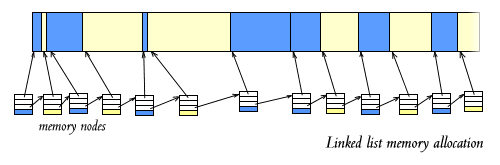

To allocate some space, we search along the list til we find an unallocated area of memory which is big enough (typically much faster than searching a bitmap).
When we find a suitable hole, split it into two parts, enough to satisfy the request, and whatever is left over.
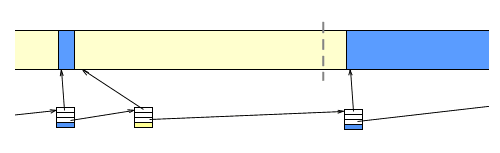
Replace the single 'hole' node in the list, with a 'allocated block' node, followed by a 'hole' node.
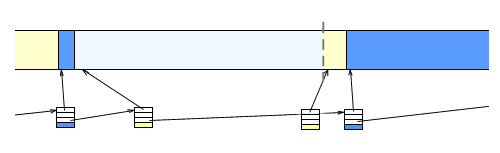
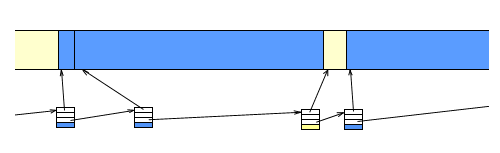
Return the address of the block.
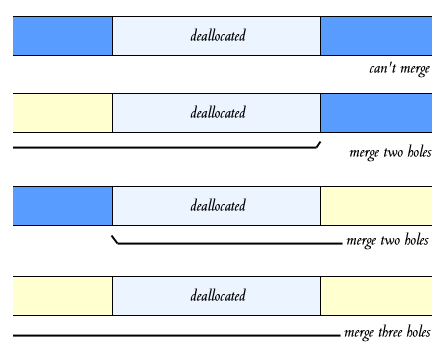
To deallocate memory, we can just change its list node from 'allocated' to 'hole'.
Obviously (hopefully), if we've just created a 'hole' next to another 'hole', we can merge the two hole nodes. In fact, if we've just deallocated some memory, the memory above and below it (the nodes after and before it), might be allocated, or might be free. If we deallocate some memory between two holes, we can merge all three holes, into one big hole.
This is the basic algorithm, but there are several variations on the theme. Firstly, there is the choice as to how we search the list:
The simplest way is just to wonder along til we find a hole which is big enough. It's quite fast (as fast as possible with the simple linked-list algorithm we've just described).
Another possibility is to find the smallest hole which will possibly satisfy the request; the snuggest fit of all the holes in the linked list. Best fit tries to avoid breaking up large holes which may be required later.
Unfortunately, best fit tends to produce lots of small, useless holes, and surprisingly, wastes more memory this way than does first fit.
In response to best fit creating lots of small, useless holes, an alternative approach might be to find the biggest hole each time---the 'worst' fit for the requested memory allocation---and allocate from that. All the holes this produces should be large and useful.
Unfortunately, this doesn't work very well either.
Then we have the choice of how to arrange the list. The list structure we mentioned, which has all the nodes---blocks and holes---linked in order of memory address is simple and efficient. Merging holes is easy.
If we know that some sizes of block are very commonly allocated, we might keep several lists, one for each common block size, and perhaps another list of miscellaneous sizes. This makes allocation at these common sizes a lot faster. The disadvantage is that we no longer have the hole lists in order of memory address, so it is difficult to detect if two holes are adjacent in memory and may be merged into one hole.
A similar approach might be to sort the hole list in increasing order of size. This means that the first fit search automatically becomes a best fit search. It has two disadvantages: best fit isn't ideal, and again it is difficult to merge adjacent holes.